Abstract
Turbulent flow results from the erratic change in velocity and direction of a fluid flow over time. Hence producing irregular mixing and increased transport processes during the flow. Especially for those relying on passive heat transfer methods, designing efficient thermal energy systems requires an awareness of turbulent natural convection. This study aims to find how Rayleigh number affects flow pattern and heat transfer features by focusing on two-dimensional turbulent natural convection within a cylindrical enclosure. The enclosure examined employs Reynolds-Averaged Navier-Stokes (RANS) equations in conjunction with the energy equation, turbulence transport equations, and the Boussinesq approximation to represent buoyancy effects. The top wall is maintained at a consistent 298 K (ambient room temperature), while the bottom wall is regularly heated to 320 K; the vertical sidewalls are insulated. To properly represent turbulent features, a two-equation turbulence model appropriate for low Reynolds number flows is used. Numerical simulations are run with the Prandtl number fixed at 0.71—that of air—using a finite difference approach inside ANSYS Fluent. The obtained results revealed that the velocity and temperature decrease with increasing the aspect ratio (AR = 1, 2, 4, 8) at fixed Ra. Both maximum velocity and maximum temperature reduce with AR increase from 0.808 to 0.3090 m/s and from 192K to 55.6 K, while higher AR produces weaker convection, lower turbulence intensity, and more pronounced thermal stratification. Even with uniform Ra, the flow characteristics and heat transfer effectiveness are determined solely by the geometry. This illuminates the controlling influence of aspect ratio in confined natural convection systems.
Keywords
Localised Heating and Cooling, Turbulent Flow, Aspect Ratio, Velocity and Temperature Distributions
1. Introduction
Natural convection heat transfer is a topic that many folks find interesting. It's all about how fluids move due to changes in temperature. So, when we talk about natural convection, we're really looking at fluid motion that happens because of differences in density. This happens when the fluid is heated or cooled. The buoyancy forces push the fluid up or down. Imagine a pot of water on the stove: the warmer water at the bottom rises, while cooler water sinks.
| [9] | Mayoyo, R., Sigey, J. K., Okelo, J. A., & Okwoyo, J. M. (2015). An investigation of buoyancy driven natural convection in a cylindrical enclosure. |
[9]
.
Natural convection has become quite popular in cooling systems, especially within electronic devices. When lots of small thermal connections are crammed together on a tiny base, natural convection proves to be reliable and cost-effective.
| [1] | Awuor K. O (2013) Turbulent natural convention in an enclosure: Numerical study of different models. PhD thesis, Kenyatta University. |
[1]
Recently, researchers have taken a keen interest in how convection and mass transfer work around cylindrical shapes. Cylinders play a key role in things like nuclear waste disposal and certain industrial processes. You often see turbulent natural convection flow around these vertical cylinders in several technologies.
| [7] | Lee, J. M., Ha, M. Y., & Yoon, H. S. (2010). Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations. International Journal of Heat and Mass Transfer, 53(25-26), 5905-5919. |
[7]
. For example, space heaters and various electronic systems depend on this kind of flow.
In essence, natural convection is driven by buoyancy due to the temperature differences in fluids
| [1] | Awuor K. O (2013) Turbulent natural convention in an enclosure: Numerical study of different models. PhD thesis, Kenyatta University. |
[1]
. It’s super important for heat transfer—it pops up all over. Think about electrical components, heat exchangers, and more—natural convection is there. Now let’s talk about the laws governing this process. They are based on some basic principles like mass conservation and energy conservation (plus some thermodynamic laws too). When fluid flows near a wall, it must follow certain rules. Near the wall, it doesn’t slide; its velocity goes to zero right there.
On the flip side, turbulent flows can be quite chaotic and unpredictable. Unlike laminar flow—which is smooth—turbulent flow has eddies that mix everything up. These eddies can be quite large or very small. These swirling movements make it tricky to solve equations related to them. In fact, solving turbulent flow problems can get pretty complicated because there are often more unknowns than equations to figure them out. There are models that help reduce these unknowns. They’re not perfect either. When it comes to flows with high Reynolds numbers—that usually means they’re turbulent—while those with low numbers tend towards being laminar.
You can switch from smooth to turbulent flow by doing something simple like adding roughness to a surface. This little trick can change how fluid moves quite dramatically. The goal of our study is that we want to look at how temperature changes and velocity profiles affect heat transfer inside a cylindrical enclosure. We’ve got a convection heater on the floor and cooling on opposite wall.
2. Literature Review
Here are some reviews of studies that other authors have done in enclosures.
Shin, H. S. and friends
| [14] | Shin, H. S., & Kim, D. K. (2024). Experimental study on natural convection from vertical cylinders with perforated plate fins. Applied Thermal Engineering, 123768. |
[14]
looked into how heat escapes from vertical cylinders with these fabulous perforated plate fins. They tested a total of sixteen finned cylinders! Each one was different in some way. They wanted to see how things like the size, how many fins were there, and how hot the base was compared to the base air around it affected heat transfer. They figured out some new ways to predict the Nusselt number. This number is significant when we talk about heat transfer analysis. With these new ideas, they built a thermal model that could guess how well these perforated-finned cylinders would work. It had less than a 10% error in predictions. When they added perforations to the fins, it improved the thermal performance of those vertical cylinders by 13%.
Rostami, J.
| [12] | Rostami, J. (2024). Unsteady Heat Transfer in Cylindrical Encapsulated Phase Change Materials with Buoyancy Effect. Journal of Heat and Mass Transfer Research, 11(2), 225-236. |
[12]
. Examined buoyancy influences on unsteady heat transfer within cylindrical materials undergoing phase changes—in two pipes situated in channel flows using Boussinesq approximation methods for simulation purposes! This area is pertinent when considering air conditioning applications; they tried calculating discharge times for PCM (phase change Material), utilizing ice-based PCM within those pipes as coolant. Results indicate discharge times hitting impressively around 4,000 for Gr = 5,000 and 70,000 for Gr = 200,000. Meanwhile, kr values showed differences too—from 25,000 up to 34,000 depending on specific conditions like Cpr values—ranging from 11K through a high of 28K—but still echoing lumped temperature assumptions around PCM results because buoyancy force encouraged fine mixing throughout materials.
Rahaman et al.
| [16] | Rahaman, M. M., Bhowmick, S., Ghosh, B. P., Xu, F., Mondal, R. N., & Saha, S. C. (2023). Transient natural convection flows and heat transfer in a thermally stratified air-filled trapezoidal cavity. Thermal Science and Engineering Progress, 40, 102377. |
[16]
Conducted numerical study of intermittent natural convection and heat. Two-dimensional, air-filled trapezoidal cavity with a heated bottom, cooled top, and Inclined walls with thermal stratification. The investigation examined the impacts of the Finite Volume Method. Varying Rayleigh numbers to investigate flow behavior and a constant Prandtl number of 0.71 thermic effectiveness. The results showed complicated bifurcation events including pitchfork and Hopf bifurcations and a shift to chaos. Heat transfer studies revealed a notable link with Enhancement of knowledge on thermally stratified convective systems through Rayleigh number.
Employing the Finite Volume Method, Rahaman et al.
| [17] | Rahaman, M. M., Bhowmick, S., & Saha, S. C. (2023). Thermal performance and entropy generation of unsteady natural convection in a trapezoid-shaped cavity. Processes, 13(3), 921. |
[17]
investigated the impacts of Rayleigh numbers ranging from 10 to 14 and a Prandtl number of 7.01 on flow patterns, temperature profiles, and thermal performance in a trapezoid-shaped cavity filled with thermally stratified water. Results showed changes from steady to turbulent flow with pitchfork, Hopf, and chaotic bifurcations found between certain Ra ranges. Over the tested Ra spectrum, entropy generation increased by 94.97% and the Nusselt number by 81.13%. Against earlier research, the findings of this study were confirmed to improve knowledge of stratified convection systems.
Gautam et al
| [4] | Gautam, S., Khan, M. J., Khan, A., Sharma, V., Farid, F., & Sharma, A. K. (2022). Enhancement of Natural Convection Heat Transfer in Cylindrical Enclosure with Internal Heat Source. In Recent Advances in Manufacturing, Automation, Design and Energy Technologies: Proceedings from ICoFT 2020 (pp. 983-992). Springer Singapore. |
[4]
looked at improving natural convection heat transfer in a round container with a built-in heat source. Using a chimney helped move heat away from this source faster. To get more heat out of the plate using air, any plate with at least one hole could work. But, when it comes to liquid sodium, using a funnel chimney arrangement gave the best results for heat transfer.
Ong’era, O. G et al
| [11] | Ong’era, O. G., Sigey, J. K., Okelo, J. A., & Karanja, S. M. (2021) Analysis of Turbulent Natural Convection with Localized Heating on the Ceiling and on the Floor and Cooling on Opposite Vertical Walls in a Rectangular Enclosure. |
[11]
Studied investigation on turbulent natural convection in a rectangular inclusion that had heating on the ground floor and top. In contrast, cooling occurred on the walls opposite this heat source. The outcomes showed that as the Euler number increased, fluid velocity went up. Also, if the Reynolds number rose, the temperature dropped. Interestingly, increasing the Froude number led to reduced velocity as the room height got taller.
Laidoudi, H.
| [6] | Laidoudi, H., & Ameur, H. (2021). Investigation of the natural convection within a cold circular enclosure containing three equal-sized cylinders of hot surface. In Defect and Diffusion Forum (Vol. 409, pp. 49-57). Trans Tech Publications Ltd. |
[6]
Investigated how natural convection affects fluid movement and heat transfer. This was done with four heated circular cylinders sitting inside a circular space that had a cold surface. These cylinders were placed across from each other, which is interesting. During the tests, they used different starting conditions and came up with some cool results. The Prandtl number varied from 7.1 to 1000, and the Rayleigh number ranged from
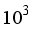
to
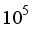
. They also figured out the average Nusselt number for each inner cylinder. Plus, the study looked at how strong thermal buoyancy affected fluid movement & temperature. The findings showed something important: the heat transfer rate really changes based on where the cylinders are in the enclosure. When it comes to the Prandtl number, its effect on flow and heat patterns was pretty small.
Medebber, M. A. et al
| [10] | Medebber, M. A., Retiel, N., Aissa, A., & El Ganaoui, M. (2020). Transient numerical analysis of free convection in cylindrical enclosure. In MATEC Web of Conferences (Vol. 307, p. 01029). EDP Sciences. |
[10]
Investigated free convection in a vertical cylinder over time, using numerical methods to analyze it in two dimensions. They had an adiabatic top and bottom walls and uniform temperature across those walls. They used Rayleigh numbers between
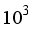
and
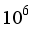
with height ratios at 0.5 and Prandtl numbers around 7.0 to see how various factors influenced average Nusselt numbers and flow patterns.
Muia M. and K. A
| [8] | Muia M. and K. A.(2018) Numerical simulation of turbulent natural convection of air in a rectangular enclosure, World Journal of Natural Sciences Research, vol. 8, no. 6, pp. 24–31. |
[8]
The focus here was on studying turbulent natural air convection in a rectangle enclosure using numerical modeling. The horizontal surfaces stayed at steady temperature of 40K, and the other remaining walls were kept adiabatic. Interestingly, as they increased the aspect ratio, eddies started showing up in both heated and cooled areas at the top and bottom.
Enayati H et al
| [3] | Enayati, H., Chandy, A. J., & Braun, M. J. (2016). Numerical simulations of turbulent natural convection in laterally-heated cylindrical enclosures with baffles for crystal growth. In ASME International Mechanical Engineering Congress and Exposition (Vol. 50626, p. V008T10A052). American Society of Mechanical Engineers. |
[3]
Studied how natural convection works when heat is added to the sides of cylindrical spaces used for crystal growth. Inside these cylinders, free convection happens because of the heat. The author looked at a range for Ra between 750 and 8.8 x
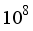
. This number helps to describe how the size of the cylinder relates to its heated surface area. They used a computer program called FLUENT. It solved important equations by breaking them into smaller parts using a finite volume method. The way pressure and speed worked together was managed by an algorithm called PISO. A unique second-order implicit time-stepping technique was used to look at flow those changed over time. When handling the momentum, energy, and turbulence calculations, they chose the QUICK scheme. This ensured that any changes in flow direction upstream were captured accurately. The results showed that the boundary layer gets thinner when the Rayleigh number increases. This means temperature spreads out more evenly across the whole cylinder.
Mayoyo et al.
| [9] | Mayoyo, R., Sigey, J. K., Okelo, J. A., & Okwoyo, J. M. (2015). An investigation of buoyancy driven natural convection in a cylindrical enclosure. |
[9]
Researchers used a cylindrical container to look into how heat moves around. They cooled the top surface of this vertical cylinder while heating up the bottom. The walls of the cylinder were thought to be adiabatic during the test, which means no heat transfer happened there. To tackle this, they used something called the finite difference method to figure out the nonlinear governing equations. These equations were tricky since they relied on the Boussinesq approximation. After running their tests, they analyzed the results and created graphs to help show what they found. One important discovery was about buoyancy forces. These forces came from the temperature difference between the bottom parts of the cylinder. They really changed how fast the air moved inside that little enclosure.
Space V. C. C. P. A.
| [15] | Space, V. C. C. P. A. (2014). Numerical Simulation of Natural Convection in a Vertical Conical Cylinder Partially Annular Space. American Journal of Energy Research, 2(2), 24-29. |
[15]
Explored natural convection inside a conical cylinder that was vertical and partly annular spaced through numerical computation methods. They examined how isotherms and flow lines change under different boundary conditions & Rayleigh numbers, focusing on how changing the height of the inner vertical cylinder affects flow & temperature distribution.
Awuor K. O.
| [1] | Awuor K. O (2013) Turbulent natural convention in an enclosure: Numerical study of different models. PhD thesis, Kenyatta University. |
[1]
Researched on three turbulence models regarding turbulent fluid flow in an enclosed space involved the k − epsilon, k − omega, and k − omega − SST models assessing non-linear parts in averaged momentum & energy equations. Throughout their tests, they found that the k − ω − SST model did better in the results produced than its counterparts—k − ε and k − ω models. Simulations of heating/cooling showed three distinct areas: one cool area above, one warm below plus another hot region next to wall heaters or windows.
Hassan K. and J. M. Al-lateef
| [5] | Hassan, A. K., & Al-lateef, J. M. (2007). Numerical simulation of two dimensional transient natural convection heat transfer from isothermal horizontal cylindrical annuli. Journal of Engineering, 13(02), 1429-1444. |
[5]
looked into two-dimensional changes in natural convection on heat transmission from a warm cylinder that was horizontal. It focused on how diameter ratios affect fluid flow patterns—like temperatures and velocity—along with Nusselt numbers. The results were consistent with earlier studies.
Saraç B et al
| [13] | Saraç, B., Aksu, E., Demirtaş, C., & Ayhan, T. (2024). Free convection heat transfer and buoyancy-assisted flow over a heated plate inserted horizontally in a vertical channel with time-varying conditions. Journal of Thermal Analysis and Calorimetry, 149(5), 2255-2271. |
[13]
looked into heat transfer through free convection and buoyancy-assisted flow around a heated horizontal plate placed inside a vertical channel, changing over time. This research focused on how buoyancy-assisted flow behaves over this hot plate under different scenarios. This involved one alone and another involving slanted plates and different placements of these plates. Temperature differences caused airflow due to buoyancy, which varied depending on plate angles and positions, leading them to explore how these elements influenced time-dependent heat transfer coefficients.
Cheng T. C. et al.
| [2] | Cheng, T. C., Li, Y. H., & Lin, T. F. (2000). Effects of thermal boundary condition on buoyancy driven transitional air flow in a vertical cylinder heated from below. Numerical Heat Transfer: Part A: Applications, 37(8), 917-936. |
[2]
Examined how thermal boundary conditions affected airflow caused by buoyancy in a heated vertical cylinder. Their research showed multicellular vortices inside the insulated side of the cylinder. These vortices were quite asymmetric, even when things seemed steady. Interestingly, these buoyancy-driven asymmetric vortices help us understand the complicated airflow patterns under various thermal conditions. This study really deepens our knowledge about natural convection in closed spaces.
3. Statement of the Problem
Industries around the world are growing fast. It’s exciting, but designing solid and effective structures is a big issue. We need better enclosures to tackle engineering challenges. Well, it’s all about where we put the heaters and windows. The temperature and airflow depend a lot on their positions. Sadly, many existing cylindrical enclosures struggle because they don’t perform well in thermal management. Most research so far has looked at horizontal cylinder shapes. This study is different, and we want to fill the gap by checking how natural convection works in cylindrical shapes when they get hot or cold. Imagine this: a heater is on the floor, and the cooling system is on the opposite side. We will closely examine buoyancy effects, different materials that don’t let heat escape (like adiabatic material), & tweak the cooling systems too.
4. Specific Objectives of the Study
The specific objectives of the study are to:
1) Model governing equations in turbulent natural convection in a cylindrical enclosure.
2) Determine the temperature distribution and velocity profile in the cylindrical enclosure.
3) Determine the effect of Rayleigh number on fluid flow.
5. Justification of the Study
In earlier studies, researchers have looked into heating setups, too. For instance, heating on the floor with a heater placed right next to a window on the same wall or two heaters on opposite sides with windows elsewhere. These setups have different uses, but this study wants to explore new shapes. What we’re after is finding an intelligent design that combines heating from the floor with cooling systems on opposite vertical walls of cylindrical enclosures. Plus, we'll analyze what we think will happen with the natural convection under turbulent conditions.
6. Significance of the Study
Turbulent flows are prevalent in both engineering applications and natural phenomena. Turbulent natural convection, in particular, plays a critical role in various heat transfer processes. It is a fundamental mechanism in systems such as refrigerating coils, hot radiators, and the cooling of electronic devices. Moreover, it significantly impacts heating and cooling in buildings and is integral to safety applications where precise thermal management is crucial.
In industrial settings, the demand for increased productivity and competitiveness necessitates the development of innovative engineering solutions. These solutions are deeply rooted in the accurate mathematical modeling of fluid dynamics. A thorough understanding of fluid behavior allows industries to predict fluid flow patterns with high precision, leading to optimized system designs and improved operational efficiency.
Temperature distribution and fluid velocity within a given space are often critical parameters. These factors influence not only the efficiency of thermal systems but also the comfort and safety of environments where humans reside or work. In agriculture, understanding convection patterns can enhance crop management and storage conditions. Similarly, in the food industry, maintaining optimal temperatures is vital for preserving the quality of stored products. Sensitive equipment, especially in technological and scientific fields, requires precise thermal regulation to ensure proper functionality and longevity.
This study is dignified to make a meaningful contribution to the field by advancing the understanding of turbulent natural convection. By accurately predicting velocity and temperature distributions within a rectangular enclosure, the research aims to provide insights that can be applied to improve thermal management systems across various industries. The outcomes of this study have the potential to enhance human comfort, agricultural productivity, food preservation, and the reliability of sensitive equipment, thereby benefiting a broad spectrum of applications and stakeholders.
7. Mathematical Formulations
Let's discuss the equations that help us understand a 2-D cylindrical space. These include continuity, momentum in the theta & z directions, and energy equations related to turbulent kinetic energy and how it dissipates.
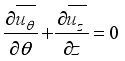 (1)
(1) 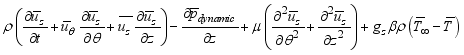 (2)
(2) 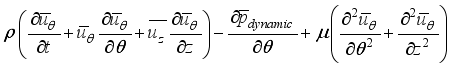 (3)
(3) 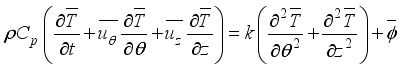 (4)
(4) Where
Where
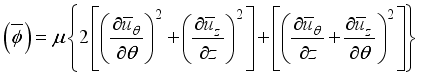
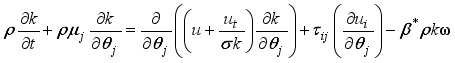 (5)
(5) 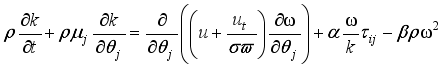 (6)
(6) Non-dimensionalization; this technique simplifies looking at complex systems. By taking away units of measurement, we can express things using dimensionless numbers. This mostly helps clear things up! With fewer parameters in our equations, it's easier to see how the system behaves.
To do this non-dimensionalization, we use specific scaled variables
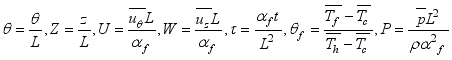 (7)
(7) Non-dimensionalized equations become
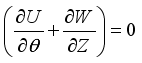 (8)
(8) 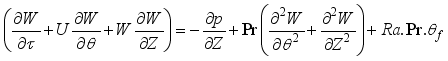 (9)
(9) 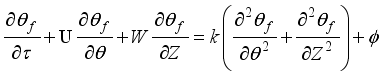 (10)
(10) Pr means the Turbulent Prandtl Number, while Ra stands for the Rayleigh Number.
7.1. Equations in Vorticity Stream Function Form
This is where we write out the dimensionless governing equations. In this form, we skip the pressure term found in the momentum equation. By doing that, we get new equations that let us figure out temperature values & unknown velocities using the vorticity stream function approach.
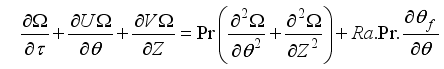 (11)
(11) 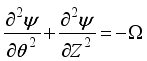 (12)
(12) 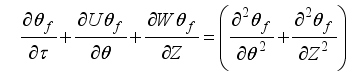 (13)
(13) Mathematical model
Figure 1. Geometry of the problem.
This is a schematic figure of the problem under study and its coordinates. The bottom side is hot (320k), and the top wall is maintained at (298k). The vertical walls are adiabatic. Since equations
11 and
13 are similar, they can be expressed as a single equation. Mobedi, M.
| [18] | Mobedi, M. (1994). A three-dimensional numerical study on natural convection heat transfer from rectangular fins on a horizontal surface [Doctoral dxaissertation, Middle East Technical University]. |
[18]
.
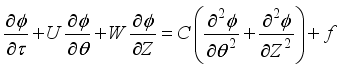 (14)
(14) 7.2. Finite Difference Solution Technique
This method enables you to define the values of the dependent variables in an identified differential equation at any discrete location in the computational domain. The finite difference approach uses the Taylor series expansion to express a variable's derivatives as the differences between values at distinct points in space or time.
Figure 2 shows the change of 𝑢 with respect to
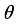
, that is 𝑢(
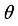
). After discretization, the curve (
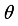
) can be represented by a set of discrete points 𝑢′𝑠. These distinct points can be connected to one another via a Taylor series expansion. Lets Consider two points (+ 1) and (𝑖 − 1).. a very small distance ∆
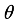
from central point denoted by (𝑖).
Figure 2. Location of points as per Taylor’s series.
The velocity
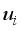
in the Taylor series expression about (𝑖) is:
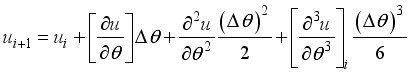 (15)
(15) and
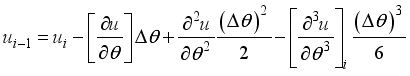 (16)
(16) If the number of terms is infinite but small, the derivative equation is mathematically precise. We express the second order accuracy and we get the truncation error as below:
By subtracting equation
16 from equation
15 we get first and second derivatives at the central position 𝑖, these derivatives are
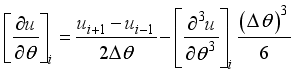 (17)
(17) And
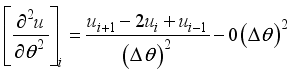 (18)
(18) Equation (
17) and (
18) are referred to as the central difference equation for the first and second derivatives respectively. Further derivatives can also be formed by considering equation
15 and equation
16 separately. Looking at equation 16 the first order derivative can be formed as
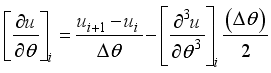 (19)
(19) This is known as the Forward difference. Similarly, from equation
15 and
16 another second order derivative can be formed as shown below
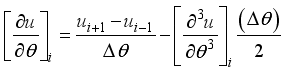 (20)
(20) This is known as the backward difference.
A Finite Difference Method is distinguished by its approximation
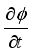
and spatial
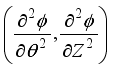
partial derivatives in the governing equation, which relate the values of the unknown function as a set of surrounding grid points at distinct time levels. This approximation substitutes the Partial Differential Equation (PDE) with a Finite Difference Equation (FDE). The process of replacing the PDE with an algebraic FDE is known as Finite Difference discretization or approximation. Finite Difference discretization consists of two steps: discretization of the solution domain and discretization of the governing equations.
7.3. Discretizing the Solution Domain
Turbulent natural convection in an enclosure is distinguished by a thin boundary layer along the walls, while the core is thermally stratified. The flow gradient in the boundary layer is very considerable, necessitating the use of a large number of grid points or computational nodes to calculate the values of dependent variables. The primitive variable is employed in this study; hence a staggered finite difference grid scheme is unnecessary. The solution's domain, or enclosure, is partitioned into a network of uniform rectangular grids with very fine spacing.
Figure 3. A two dimensional computational grid.
Figure 3 shows a two dimensional computational grid which is organized into small sections, each having a node at the middle. In a two-dimensional computational domain, each node (𝑖,) has four surrounding nodes, as seen in the diagram below.
Figure 4. A node of (i, j) with the neighboring nodes.
Discretizing the Governing Equations
In order to create a system of linear algebraic equations that relate the value of the unknown function ∅ at the nodes, the governing equations must be substituted by a finite difference equation, which is the n applied successively at the internal nodes of the grid. Producing the values of the function ∅ at the nodes (𝑖) is the aim of PDE using the FDE.
Figure 5. A three- point difference approximation.
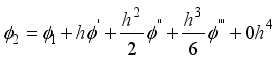 (21)
(21) 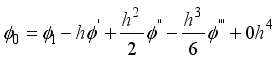 (22)
(22) Finding the difference by Subtracting equation (
22) from equation (
21) yields
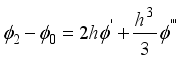 (23)
(23) Making
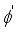
the subject and rearranging
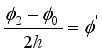 (24)
(24) Adding equation
21 to equation
22 gives
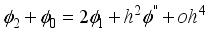 (25)
(25) Making
the subject and rearranging
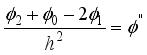 (26)
(26) Where h is the spacing of the grid
By approximating the time derivative
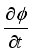
using a first order backward difference approach about a grid point (𝑖,) at the time instant
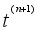
using Taylor's series expansion in 𝑡, we get
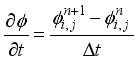 (27)
(27) Using Taylor's series expansions for approximating spatial derivatives with second-order centered difference, we get:
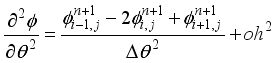 (28)
(28) and
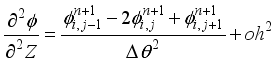 (29)
(29) The described approach is first-order accurate in time and second-order accurate in space. It approximates the spatial derivatives at a node, based on the dependent variable at the node and the neighboring cells, making this method change an n-equation differential equation into an n-equation algebraic one. The solution of this equation gives the value of the variable at the node. In the case of time-dependent problems, the domain has to be additionally discretized in time using a specified time step.
7.4. Finite Difference Solution Method for Parabolic Differential Equations
Equation
14 is reduced to;
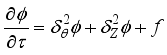 (30)
(30) Where
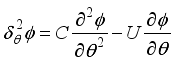 (31)
(31) 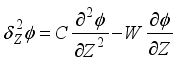 (32)
(32) Diffusion and convection are important concepts. The terms
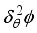
is the diffusion and convection transport in
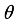
the direction while
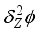
referring to diffusion and convection transport in the Z direction.
There are several finite difference methods when it comes to solving parabolic partial differential equations. Usually, we can organize these methods into three main groups: the implicit, the explicit method, and Alternating Direction Implicit (ADI). For our study, we decided to go with the explicit method.
So, what makes the explicit method interesting. Well, it moves through the dependent variable from one point to the next—node by node! However, this technique needs really small grid sizes or time intervals to stay stable. Because of that, it ends up needing a lot of computer storage and takes quite a bit of time to compute.
Applying the explicit method on equation
30 for any node (𝑖,) with a simple forward difference for the time term gives.
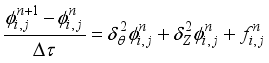 (33)
(33) 7.5. Thermal Conditions at Boundary Points
1) The study comprises heating one wall at the base and cooling the upper section of the opposing one. Two thermal conditions were utilized.
2) For vertical walls, isothermal is expressed by the equation = Constant. Applicable to both the hot and cold walls is the Dirichlet boundary condition where Θhot = 1 and Θcold = 0.
3) Adiabatic: The remaining walls temperatures stayed consistent.
7.6. Velocity Conditions at the Boundary
Slippage has no frontier condition. Because the cohesive force is smaller than the adhesive force, the air particles near the surface won't follow the stream. At the solid boundary, then, viscous fluid will have velocity nil in relation to the wall. As a result, the outside molecules of the fluid stick to the surface it passes. On the surface therefore, 𝑢 = 𝑣 = 𝑤 = 0. Free slide's boundary condition is implemented. Every limit in this cylindrical container is thought to be impermeable. This means that mass cannot pass through an impermeable solid surface since the speed connected to the surface or boundary is zero.
8. Results and Discussion
Results are presented for the increase in aspect ratio (AR = 1, 2, 4, and 8) on natural convection in a vertical cylindrical enclosure for a constant Rayleigh number (Ra) in order to isolate the influence of geometry. With increasing aspect ratio (smaller diameter with fixed height), over which the domain is narrower and higher.
1) Result showing velocity magnitude
Figure 6. Contour of velocity magnitude of Aspect ratio 1.
Figure 7. Contour of velocity magnitude of Aspect ratio 2.
Figure 8. Contour of velocity magnitude of Aspect ratio 4.
Figure 9. Velocity magnitude of Aspect ratio 8.
Discussions of Velocity Magnitude
The maximum air speed in
Figure 6 is 0.808m/s, while in
Figure 7, the maximum air speed slightly decreases to 0.783m/s; in
Figures 8 and 9, however, the maximum air speeds even decrease to 0.497m/s and 0.317m/s, respectively. Incidentally, the center of the domain corresponds to a domain in which the velocity is larger near the mixing region, as it can be seen in
Figure 7. It is evident from
Figure 6 that there are more velocity vectors and they are more parallel to each other as we increase the aspect ratio. From
Figure 9, it can be seen that the vectors are closest to parallel (all the vector tails and heads nearest each other) of any of the configurations studied here. This sequence indicates that with the aspect ratiothe flow becomes smoother and less turbulent.
When the Rayleigh number is kept constant and the aspect ratio is raised, there are remarkable variations in the flow structures and the heat transfer phenomena. The domain is narrower by increasing the aspect ratio: decrease the diameter and keep the height constant. The buoyancy-driven natural convection in this new flow geometry is stretching in the vertical direction and compressing in the horizontal direction. With the flow being transferred from one orifice to another achieving such increased hole diameter, the flow paths become longer and higher resistant, which in turn leads to the increasing viscous dissipation as well as the decrease of circulation strength. Recirculation cells are weakened because of the lack of space for the fluid to effectively turn around and thermal stratification is enhanced, further inhibiting vertical motion. These multiplicative effects produce a damping in buoyancy-driven circulation leading to a persistent and substantial reduction in the maximum velocity in the flow field, even though Ra itself remains constant.
2) Contours of Temperature Distribution (k)
An isotherm is like a line that shows areas with the same temperature or, you can think of it as a graph curve linking spots with equal heat.
Figure 10. Contours of temperature distribution of aspect ratio 1.
Figure 11. Cont2urs of temperature distribution of aspect ratio 2.
Figure 12. Contours of temperature distribution of aspect ratio 4.
Figure 13. Contours of temperature distribution of aspect ratio 8.
In the figures presented, the maximum temperatures appear adjacent to the bottom wall, being 192 K (
Figure 9), 162 K (
Figure 10), 112 K (
Figure 12), and 55.6 K (
Figure 13). The decreasing maximum temperatures correspond to an increasing enclosure aspect ratio.
In other words, in all cases two counter-rotational circular convection cells (one obverse and one reverse) are present, which can be considered evidence of natural convection. The more buoyant and heated air along the bottom wall ascends and cools as it moves upwards, which is represented by the variation in color. Mixing between two isothermal side walls leads to a region of thermal uniformity that looks cooler.
The gradually decreasing maximum temperature throughout the figures is a result of materials domain geometry variation affecting temperature distribution (i.e. increased aspect ratio proposed by decreasing diameter and constant height). With increasing AR, the heat spreads out more over the domain and becomes less localized near the heat source. This geometric layout promotes thermal diffusion characterized by lower maximum temperatures and more uniform gradients of the isotherms. In addition, increased aspect ratios lead to increased thermal stratification, where temperature encroaches more vertically with a decrease in thermal field intensity resulting in a further decrease of temperature values.
9. Conclusion
We took a good look at how natural convection works in a vertical cylinder. It was heated on one side and cooled on opposite side. We used numerical methods to into all of this. Our main goals got checked off one by one. We started with the k-ω turbulence model. Then we applied the Boussinesq approximation. This made those tricky conservation equations easier to handle.
In spite of constant Rayleigh number, which provides the buoyancy driving force the same, the dimensions of aspect ratio (height/diameter) that change by varying the diameter and maintaining the height become significantly influence to both the temperature and the velocity fields. As the aspect ratio grows, the domain becomes more long and narrow, and the buoyancy-induced circulation is weakened.
This morphology constraint results in longer flow passage, more resistance force viscous and significant drop of maximal speed. Meanwhile, the thermal field becomes more decentralized, and the heat is distributed on a larger zone to yield gradually reduced maximal temperatures. More anisotropic aspect ratios create also stronger thermal stratification, where the temperature gradients are vertically striated with reduced mixing. These results clearly demonstrate that, with a fixed Ra, the role of geometric configuration (or aspect ratio) is decisive to ensure the convective flow motion can be suppressed, turbulence can be deteriorated, and the heat transfer process can be limited.
10. Recommendations
Further investigations are recommended for:
1) At constant Rayleigh number, vary the enclosure dimensions and investigate the behavior of streamlines and isotherms distributions.
2) Determine the effect of varying the characteristics of the fluid contained in the enclosure.
3) Investigate the same enclosure with other models like k-epsilon and
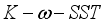
.
Abbreviations
RANS | Reynolds-Averaged Navier–Stokes |
Ra | Rayleigh Number |
K | Kelvin |
ANSYS Fluent | Computational Fluid Dynamics (CFD) Software Tool |
PDE | Partial Differential Equation |
FDE | Finite Difference Equation |
Acknowledgments
We appreciate Jomo Kenyatta University of Agriculture and Technology (JKUAT) for providing invaluable resources, technical support, and an enriching academic environment. Their contributions were instrumental in the success of this study.
Author Contributions
Omariba Geofrey Ong'era: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing
Johana Kibet Sigey: Conceptualization, Methodology, Supervision, Validation, Writing – review & editing
Jeconia Abonyo Okelo: Formal Analysis, Supervision, Validation, Writing – review & editing
Stephen Mbugua Karanja: Conceptualization, Supervision, Writing – review & editing
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
Awuor K. O (2013) Turbulent natural convention in an enclosure: Numerical study of different models. PhD thesis, Kenyatta University.
|
| [2] |
Cheng, T. C., Li, Y. H., & Lin, T. F. (2000). Effects of thermal boundary condition on buoyancy driven transitional air flow in a vertical cylinder heated from below. Numerical Heat Transfer: Part A: Applications, 37(8), 917-936.
|
| [3] |
Enayati, H., Chandy, A. J., & Braun, M. J. (2016). Numerical simulations of turbulent natural convection in laterally-heated cylindrical enclosures with baffles for crystal growth. In ASME International Mechanical Engineering Congress and Exposition (Vol. 50626, p. V008T10A052). American Society of Mechanical Engineers.
|
| [4] |
Gautam, S., Khan, M. J., Khan, A., Sharma, V., Farid, F., & Sharma, A. K. (2022). Enhancement of Natural Convection Heat Transfer in Cylindrical Enclosure with Internal Heat Source. In Recent Advances in Manufacturing, Automation, Design and Energy Technologies: Proceedings from ICoFT 2020 (pp. 983-992). Springer Singapore.
|
| [5] |
Hassan, A. K., & Al-lateef, J. M. (2007). Numerical simulation of two dimensional transient natural convection heat transfer from isothermal horizontal cylindrical annuli. Journal of Engineering, 13(02), 1429-1444.
|
| [6] |
Laidoudi, H., & Ameur, H. (2021). Investigation of the natural convection within a cold circular enclosure containing three equal-sized cylinders of hot surface. In Defect and Diffusion Forum (Vol. 409, pp. 49-57). Trans Tech Publications Ltd.
|
| [7] |
Lee, J. M., Ha, M. Y., & Yoon, H. S. (2010). Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations. International Journal of Heat and Mass Transfer, 53(25-26), 5905-5919.
|
| [8] |
Muia M. and K. A.(2018) Numerical simulation of turbulent natural convection of air in a rectangular enclosure, World Journal of Natural Sciences Research, vol. 8, no. 6, pp. 24–31.
|
| [9] |
Mayoyo, R., Sigey, J. K., Okelo, J. A., & Okwoyo, J. M. (2015). An investigation of buoyancy driven natural convection in a cylindrical enclosure.
|
| [10] |
Medebber, M. A., Retiel, N., Aissa, A., & El Ganaoui, M. (2020). Transient numerical analysis of free convection in cylindrical enclosure. In MATEC Web of Conferences (Vol. 307, p. 01029). EDP Sciences.
|
| [11] |
Ong’era, O. G., Sigey, J. K., Okelo, J. A., & Karanja, S. M. (2021) Analysis of Turbulent Natural Convection with Localized Heating on the Ceiling and on the Floor and Cooling on Opposite Vertical Walls in a Rectangular Enclosure.
|
| [12] |
Rostami, J. (2024). Unsteady Heat Transfer in Cylindrical Encapsulated Phase Change Materials with Buoyancy Effect. Journal of Heat and Mass Transfer Research, 11(2), 225-236.
|
| [13] |
Saraç, B., Aksu, E., Demirtaş, C., & Ayhan, T. (2024). Free convection heat transfer and buoyancy-assisted flow over a heated plate inserted horizontally in a vertical channel with time-varying conditions. Journal of Thermal Analysis and Calorimetry, 149(5), 2255-2271.
|
| [14] |
Shin, H. S., & Kim, D. K. (2024). Experimental study on natural convection from vertical cylinders with perforated plate fins. Applied Thermal Engineering, 123768.
|
| [15] |
Space, V. C. C. P. A. (2014). Numerical Simulation of Natural Convection in a Vertical Conical Cylinder Partially Annular Space. American Journal of Energy Research, 2(2), 24-29.
|
| [16] |
Rahaman, M. M., Bhowmick, S., Ghosh, B. P., Xu, F., Mondal, R. N., & Saha, S. C. (2023). Transient natural convection flows and heat transfer in a thermally stratified air-filled trapezoidal cavity. Thermal Science and Engineering Progress, 40, 102377.
|
| [17] |
Rahaman, M. M., Bhowmick, S., & Saha, S. C. (2023). Thermal performance and entropy generation of unsteady natural convection in a trapezoid-shaped cavity. Processes, 13(3), 921.
|
| [18] |
Mobedi, M. (1994). A three-dimensional numerical study on natural convection heat transfer from rectangular fins on a horizontal surface [Doctoral dxaissertation, Middle East Technical University].
|
Cite This Article
-
APA Style
Ong'era, O. G., Sigey, J. K., Okelo, J. A., Karanja, S. M. (2025). Analysis of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. International Journal of Fluid Mechanics & Thermal Sciences, 11(2), 20-32. https://doi.org/10.11648/j.ijfmts.20251102.12
 Copy
|
Copy
|
 Download
Download
ACS Style
Ong'era, O. G.; Sigey, J. K.; Okelo, J. A.; Karanja, S. M. Analysis of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. Int. J. Fluid Mech. Therm. Sci. 2025, 11(2), 20-32. doi: 10.11648/j.ijfmts.20251102.12
 Copy
|
Copy
|
 Download
Download
AMA Style
Ong'era OG, Sigey JK, Okelo JA, Karanja SM. Analysis of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. Int J Fluid Mech Therm Sci. 2025;11(2):20-32. doi: 10.11648/j.ijfmts.20251102.12
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.ijfmts.20251102.12,
author = {Omariba Geofrey Ong'era and Johana Kibet Sigey and Jeconia Abonyo Okelo and Stephen Mbugua Karanja},
title = {Analysis of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder
},
journal = {International Journal of Fluid Mechanics & Thermal Sciences},
volume = {11},
number = {2},
pages = {20-32},
doi = {10.11648/j.ijfmts.20251102.12},
url = {https://doi.org/10.11648/j.ijfmts.20251102.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijfmts.20251102.12},
abstract = {Turbulent flow results from the erratic change in velocity and direction of a fluid flow over time. Hence producing irregular mixing and increased transport processes during the flow. Especially for those relying on passive heat transfer methods, designing efficient thermal energy systems requires an awareness of turbulent natural convection. This study aims to find how Rayleigh number affects flow pattern and heat transfer features by focusing on two-dimensional turbulent natural convection within a cylindrical enclosure. The enclosure examined employs Reynolds-Averaged Navier-Stokes (RANS) equations in conjunction with the energy equation, turbulence transport equations, and the Boussinesq approximation to represent buoyancy effects. The top wall is maintained at a consistent 298 K (ambient room temperature), while the bottom wall is regularly heated to 320 K; the vertical sidewalls are insulated. To properly represent turbulent features, a two-equation turbulence model appropriate for low Reynolds number flows is used. Numerical simulations are run with the Prandtl number fixed at 0.71—that of air—using a finite difference approach inside ANSYS Fluent. The obtained results revealed that the velocity and temperature decrease with increasing the aspect ratio (AR = 1, 2, 4, 8) at fixed Ra. Both maximum velocity and maximum temperature reduce with AR increase from 0.808 to 0.3090 m/s and from 192K to 55.6 K, while higher AR produces weaker convection, lower turbulence intensity, and more pronounced thermal stratification. Even with uniform Ra, the flow characteristics and heat transfer effectiveness are determined solely by the geometry. This illuminates the controlling influence of aspect ratio in confined natural convection systems.},
year = {2025}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Analysis of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder
AU - Omariba Geofrey Ong'era
AU - Johana Kibet Sigey
AU - Jeconia Abonyo Okelo
AU - Stephen Mbugua Karanja
Y1 - 2025/07/10
PY - 2025
N1 - https://doi.org/10.11648/j.ijfmts.20251102.12
DO - 10.11648/j.ijfmts.20251102.12
T2 - International Journal of Fluid Mechanics & Thermal Sciences
JF - International Journal of Fluid Mechanics & Thermal Sciences
JO - International Journal of Fluid Mechanics & Thermal Sciences
SP - 20
EP - 32
PB - Science Publishing Group
SN - 2469-8113
UR - https://doi.org/10.11648/j.ijfmts.20251102.12
AB - Turbulent flow results from the erratic change in velocity and direction of a fluid flow over time. Hence producing irregular mixing and increased transport processes during the flow. Especially for those relying on passive heat transfer methods, designing efficient thermal energy systems requires an awareness of turbulent natural convection. This study aims to find how Rayleigh number affects flow pattern and heat transfer features by focusing on two-dimensional turbulent natural convection within a cylindrical enclosure. The enclosure examined employs Reynolds-Averaged Navier-Stokes (RANS) equations in conjunction with the energy equation, turbulence transport equations, and the Boussinesq approximation to represent buoyancy effects. The top wall is maintained at a consistent 298 K (ambient room temperature), while the bottom wall is regularly heated to 320 K; the vertical sidewalls are insulated. To properly represent turbulent features, a two-equation turbulence model appropriate for low Reynolds number flows is used. Numerical simulations are run with the Prandtl number fixed at 0.71—that of air—using a finite difference approach inside ANSYS Fluent. The obtained results revealed that the velocity and temperature decrease with increasing the aspect ratio (AR = 1, 2, 4, 8) at fixed Ra. Both maximum velocity and maximum temperature reduce with AR increase from 0.808 to 0.3090 m/s and from 192K to 55.6 K, while higher AR produces weaker convection, lower turbulence intensity, and more pronounced thermal stratification. Even with uniform Ra, the flow characteristics and heat transfer effectiveness are determined solely by the geometry. This illuminates the controlling influence of aspect ratio in confined natural convection systems.
VL - 11
IS - 2
ER -
 Copy
|
Copy
|
 Download
Download
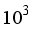 to
to 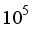 . They also figured out the average Nusselt number for each inner cylinder. Plus, the study looked at how strong thermal buoyancy affected fluid movement & temperature. The findings showed something important: the heat transfer rate really changes based on where the cylinders are in the enclosure. When it comes to the Prandtl number, its effect on flow and heat patterns was pretty small.
. They also figured out the average Nusselt number for each inner cylinder. Plus, the study looked at how strong thermal buoyancy affected fluid movement & temperature. The findings showed something important: the heat transfer rate really changes based on where the cylinders are in the enclosure. When it comes to the Prandtl number, its effect on flow and heat patterns was pretty small. 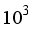 and
and 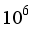 with height ratios at 0.5 and Prandtl numbers around 7.0 to see how various factors influenced average Nusselt numbers and flow patterns.
with height ratios at 0.5 and Prandtl numbers around 7.0 to see how various factors influenced average Nusselt numbers and flow patterns. 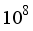 . This number helps to describe how the size of the cylinder relates to its heated surface area. They used a computer program called FLUENT. It solved important equations by breaking them into smaller parts using a finite volume method. The way pressure and speed worked together was managed by an algorithm called PISO. A unique second-order implicit time-stepping technique was used to look at flow those changed over time. When handling the momentum, energy, and turbulence calculations, they chose the QUICK scheme. This ensured that any changes in flow direction upstream were captured accurately. The results showed that the boundary layer gets thinner when the Rayleigh number increases. This means temperature spreads out more evenly across the whole cylinder.
. This number helps to describe how the size of the cylinder relates to its heated surface area. They used a computer program called FLUENT. It solved important equations by breaking them into smaller parts using a finite volume method. The way pressure and speed worked together was managed by an algorithm called PISO. A unique second-order implicit time-stepping technique was used to look at flow those changed over time. When handling the momentum, energy, and turbulence calculations, they chose the QUICK scheme. This ensured that any changes in flow direction upstream were captured accurately. The results showed that the boundary layer gets thinner when the Rayleigh number increases. This means temperature spreads out more evenly across the whole cylinder. 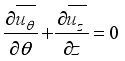 (1)
(1) 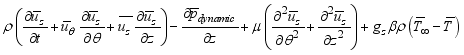 (2)
(2) 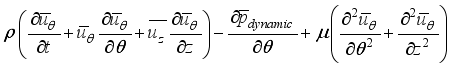 (3)
(3) 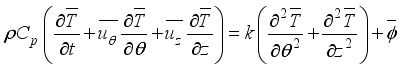 (4)
(4) 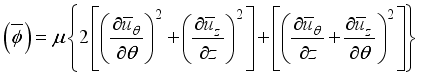
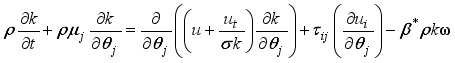 (5)
(5) 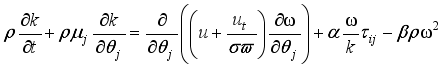 (6)
(6) 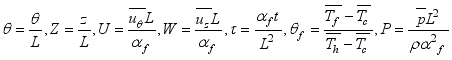 (7)
(7) 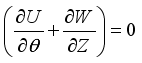 (8)
(8) 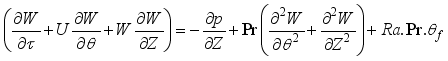 (9)
(9) 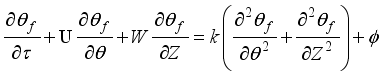 (10)
(10) 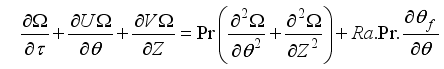 (11)
(11) 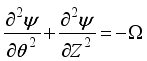 (12)
(12) 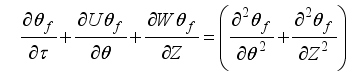 (13)
(13) 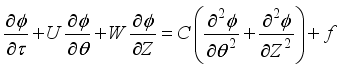 (14)
(14) 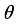 , that is 𝑢(
, that is 𝑢( 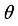 ). After discretization, the curve (
). After discretization, the curve (  ) can be represented by a set of discrete points 𝑢′𝑠. These distinct points can be connected to one another via a Taylor series expansion. Lets Consider two points (+ 1) and (𝑖 − 1).. a very small distance ∆
) can be represented by a set of discrete points 𝑢′𝑠. These distinct points can be connected to one another via a Taylor series expansion. Lets Consider two points (+ 1) and (𝑖 − 1).. a very small distance ∆  from central point denoted by (𝑖).
from central point denoted by (𝑖).  in the Taylor series expression about (𝑖) is:
in the Taylor series expression about (𝑖) is: 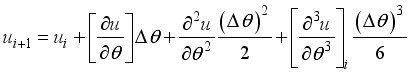 (15)
(15) 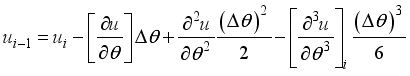 (16)
(16) 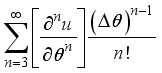
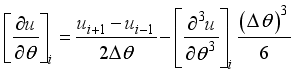 (17)
(17) 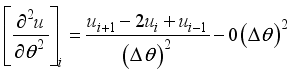 (18)
(18) 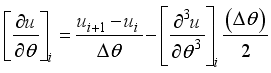 (19)
(19) 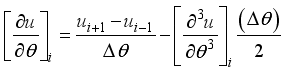 (20)
(20)  and spatial
and spatial  partial derivatives in the governing equation, which relate the values of the unknown function as a set of surrounding grid points at distinct time levels. This approximation substitutes the Partial Differential Equation (PDE) with a Finite Difference Equation (FDE). The process of replacing the PDE with an algebraic FDE is known as Finite Difference discretization or approximation. Finite Difference discretization consists of two steps: discretization of the solution domain and discretization of the governing equations.
partial derivatives in the governing equation, which relate the values of the unknown function as a set of surrounding grid points at distinct time levels. This approximation substitutes the Partial Differential Equation (PDE) with a Finite Difference Equation (FDE). The process of replacing the PDE with an algebraic FDE is known as Finite Difference discretization or approximation. Finite Difference discretization consists of two steps: discretization of the solution domain and discretization of the governing equations. 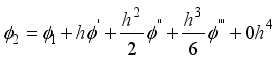 (21)
(21) 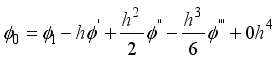 (22)
(22) 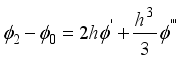 (23)
(23)  the subject and rearranging
the subject and rearranging 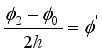 (24)
(24) 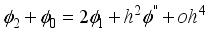 (25)
(25) 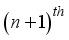 the subject and rearranging
the subject and rearranging 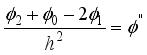 (26)
(26) 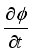 using a first order backward difference approach about a grid point (𝑖,) at the time instant
using a first order backward difference approach about a grid point (𝑖,) at the time instant 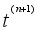 using Taylor's series expansion in 𝑡, we get
using Taylor's series expansion in 𝑡, we get 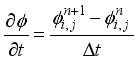 (27)
(27) 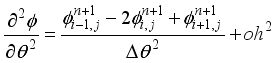 (28)
(28) 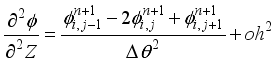 (29)
(29) 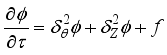 (30)
(30) 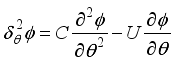 (31)
(31) 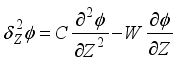 (32)
(32) 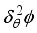 is the diffusion and convection transport in
is the diffusion and convection transport in 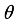 the direction while
the direction while 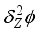 referring to diffusion and convection transport in the Z direction.
referring to diffusion and convection transport in the Z direction. 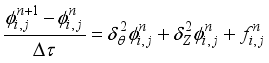 (33)
(33) 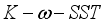 .
.